reading-notes

Linked Lists And Big O Of N

Big O notation

Big O notation is used to describe the efficiency of an algorithm or function. This efficiency depends on two factors:

  1. the amount of time the program needs to execute
  2. the memory that it takes to store data in .

Important point to understand the big O notation:

  1. Measurements of space:
    1. The amount of space needed to hold the code for the algorithm
    2. The amount of space needed to hold the input data
    3. The amount of space needed for the output data.
    4. The amount of space needed to hold working space during the calculation.

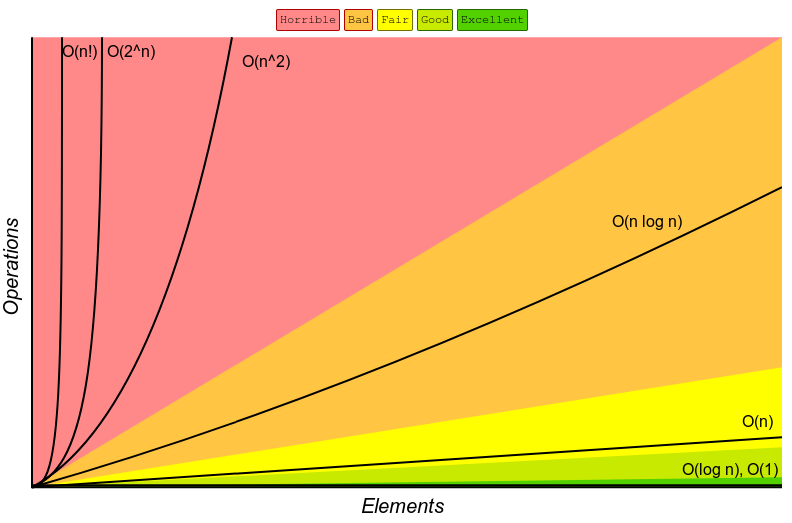
Orders of Growth

  1. O(1)

it describes the case when code will executes in the same time and space no matter what’s the inputs (constant), example:

def fact2(n):

if n == 0:
    return 1
else:
    return n * fact2(n-1)

print (fact2(5))

  1. O(N)

O(N) describes an algorithm whose performance will grow linearly and in direct proportion to the size of the input data set. for example:

def fact(n):

product = 1
for i in range(n):
    product = product * (i+1)
return product

print (fact(5))

  1. O(N²)

O(N²) represents an algorithm whose performance is directly proportional to the square of the size of the input data set. example:

a = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

for i in a:

for x in a:
    print("x")
  1. O(2^N)

O(2^N) denotes an algorithm whose growth doubles with each addition to the input data set. Example

int Fibonacci(int number)

{

if (number <= 1) return number;
   
return Fibonacci(number - 2) + Fibonacci(number - 1);  `}`

Logarithms

This type of algorithm is described as O(log N). The iterative halving of data sets described in the binary search example produces a growth curve that peaks at the beginning and slowly flattens out as the size of the data sets increase

big o

Linked Lists

A linked list is a sequence of data elements, which are connected together via links. Each data element contains a connection to another data element in form of a pointer.

Traversal Linked List

Traversing is the most common operation that is performed in almost every scenario of singly linked list. Traversing means visiting each node of the list once in order to perform some operation on that.

The pseudo-code for checking if the linked list includes a specific value is as so:

ALGORITHM Includes (value)

// INPUT <-- integer value

// OUTPUT <-- boolean

Current <-- Head

  WHILE Current is not NULL
     IF Current.Value is equal to value
  return TRUE

Current <-- Current.Next

return FALSE

verifying big o of traversal:

Adding a Node

Here are the required steps to add a new node with an O(1) efficiency:

  1. instantiate the new node that we are adding (use Add() method)
  2. newNode.Next by default is set to null. We want to set newNode.Next property to the same location that the Head node is pointing towards.
  3. At this point in the program we now “technically” have newNode at the beginning of the linked list

creation of a linked list in Python:

Example:

class Node:

def __init__(self, dataval=None):
    self.dataval = dataval
    self.nextval = None

class SLinkedList:

def __init__(self):

    self.headval = None

list1 = SLinkedList()

list1.headval = Node("Mon")

e2 = Node("Tue")

e3 = Node("Wed")

#Link first Node to second node

list1.headval.nextval = e2

#Link second Node to third node

e2.nextval = e3

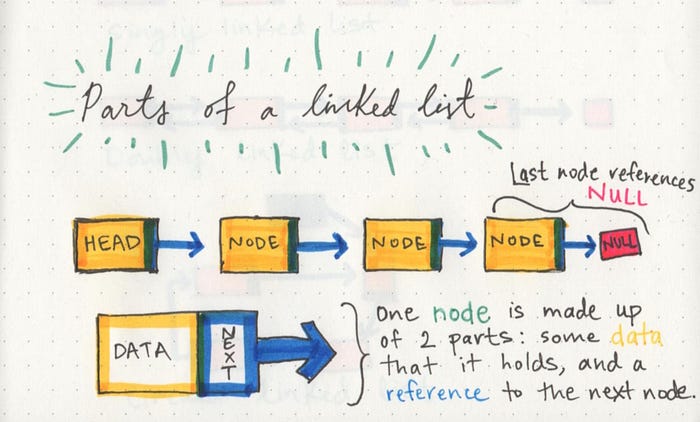
to summarize the parts of the linked list in an image:

linked list

Memory management

The biggest differentiator between arrays and linked lists is the way that they use memory in our machines.

memory